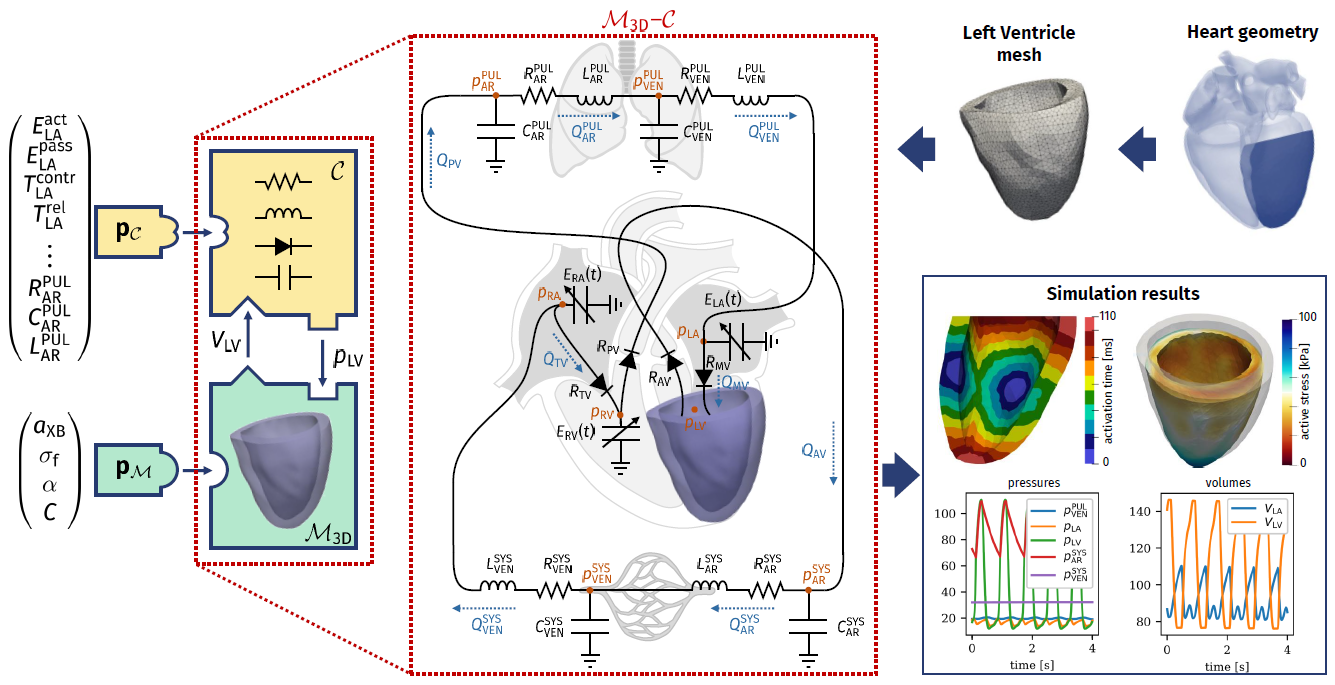
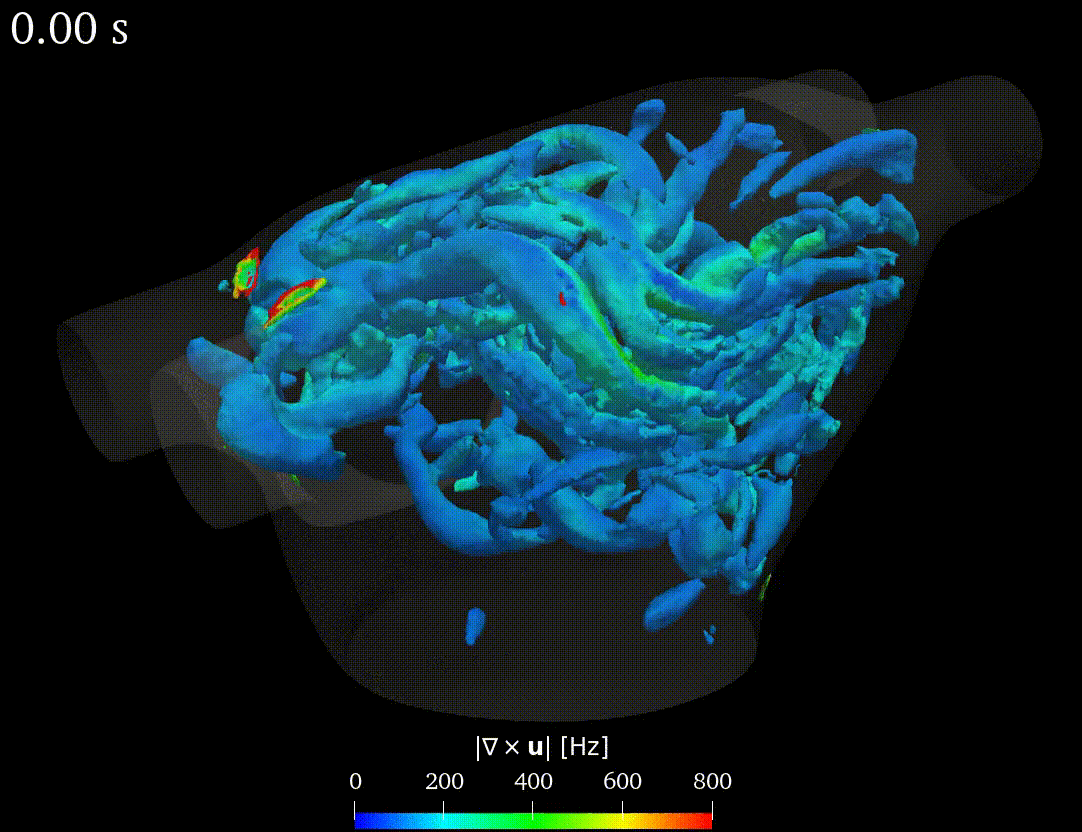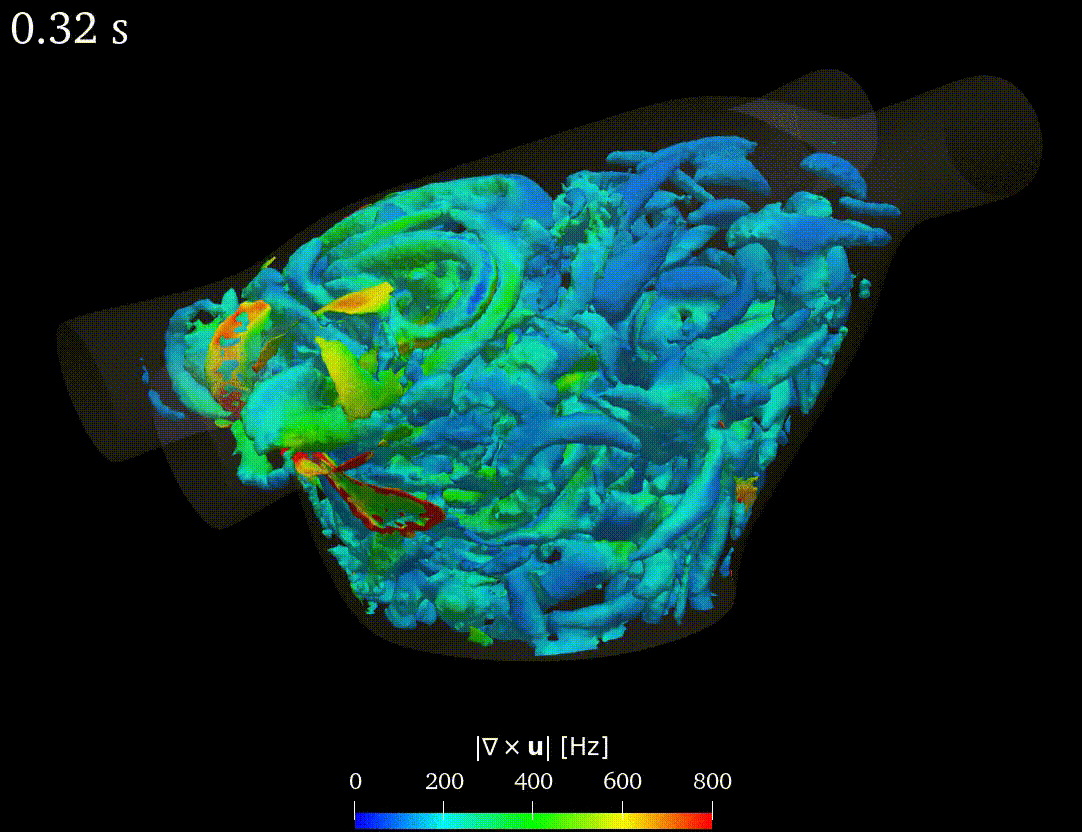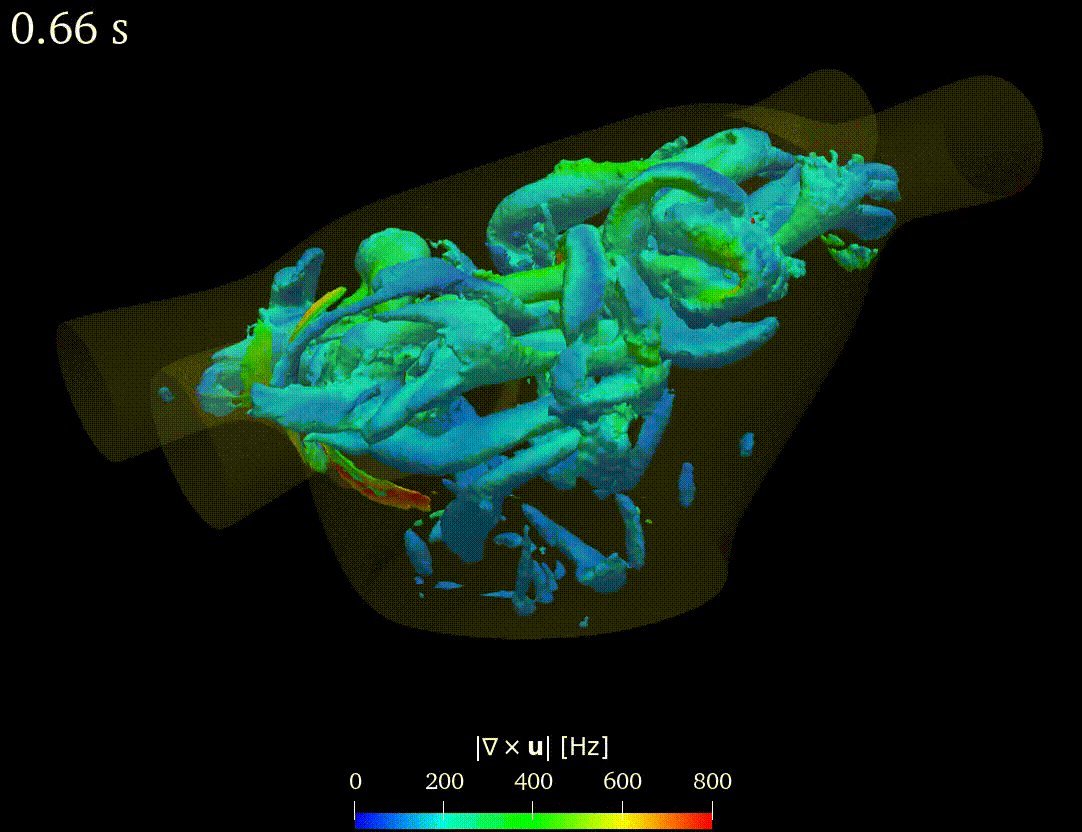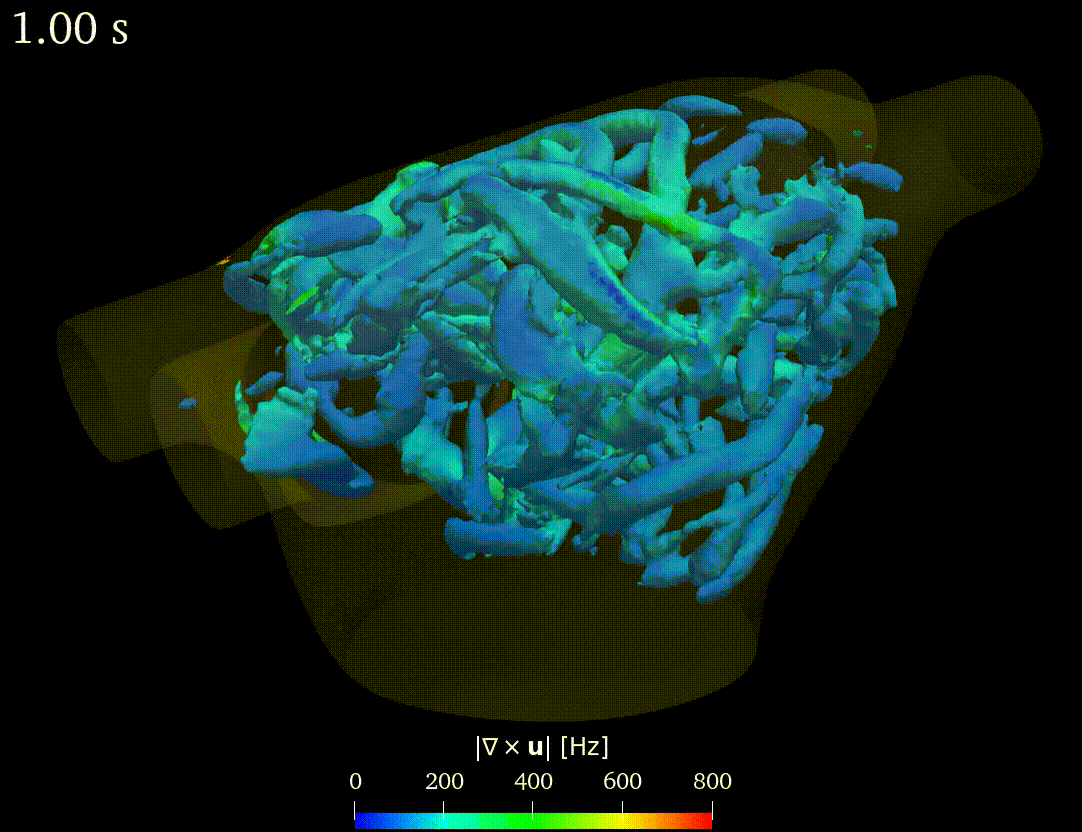
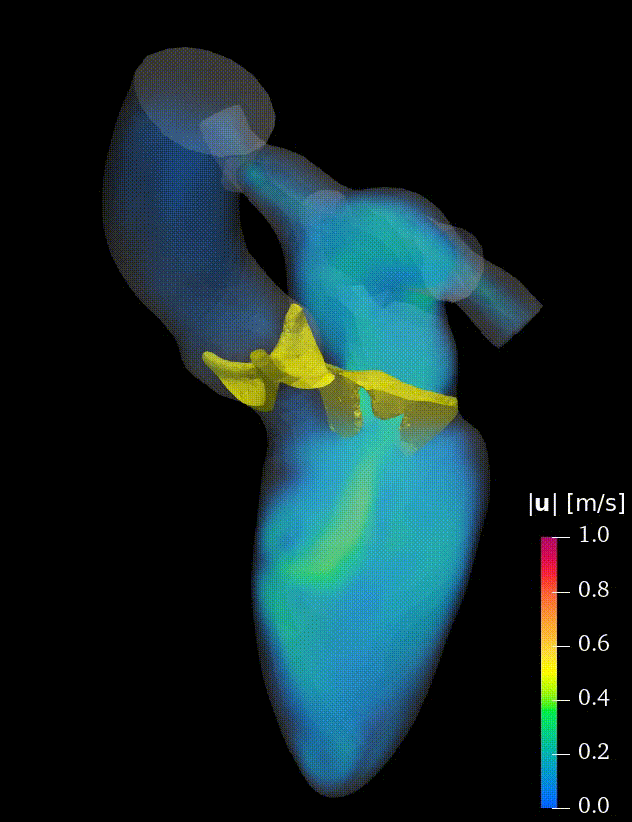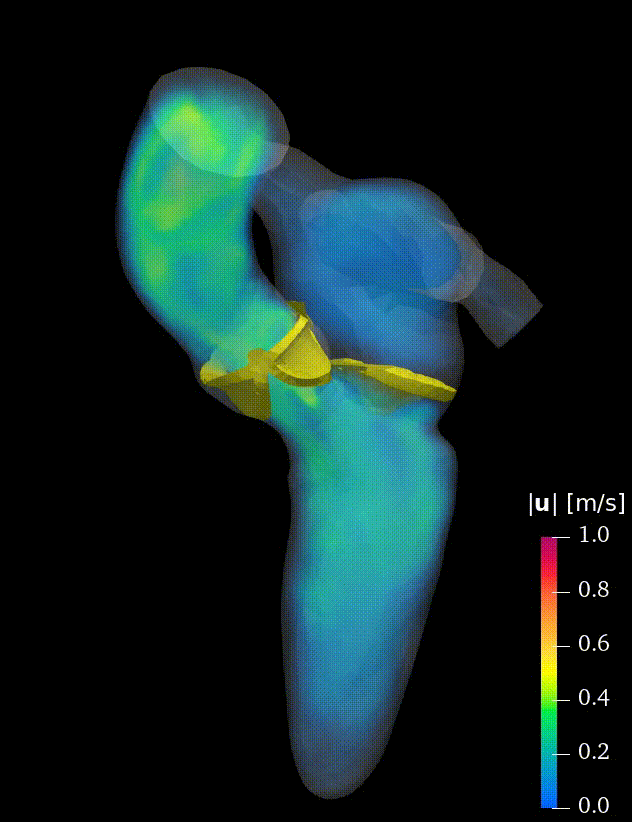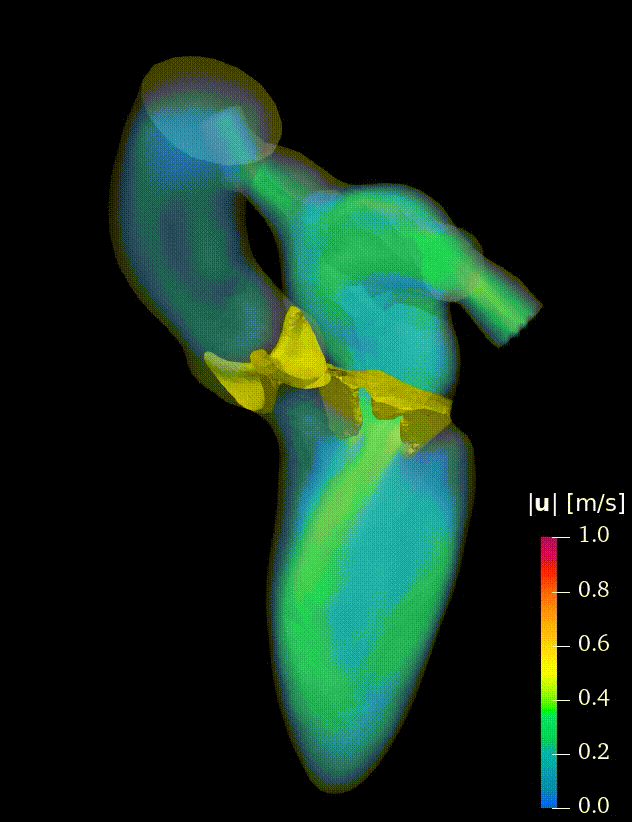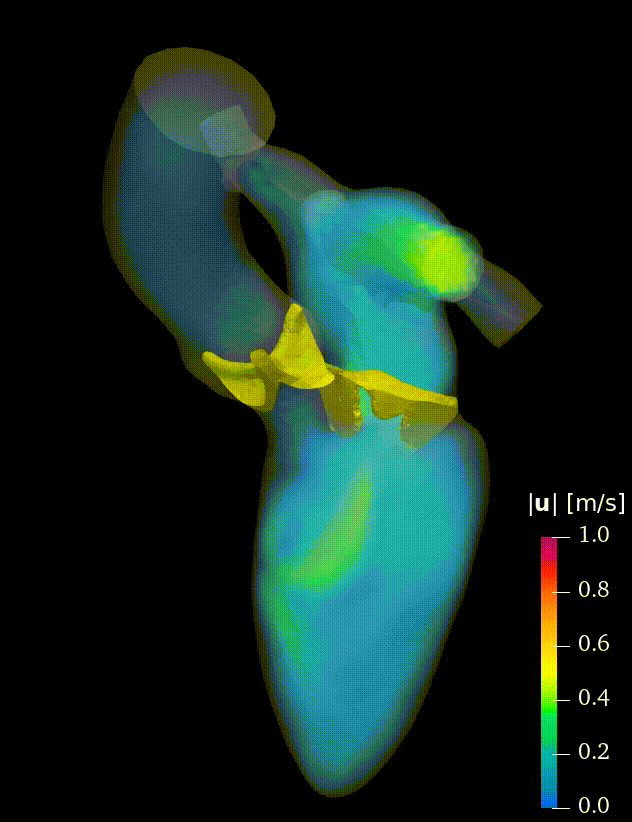
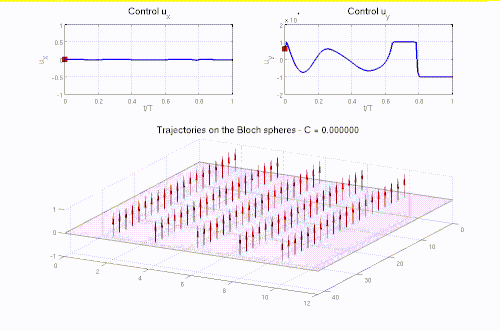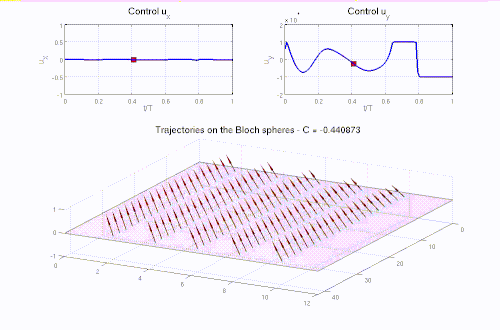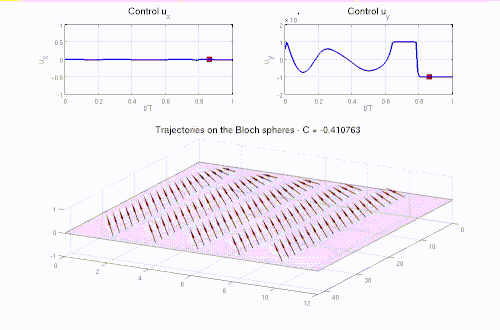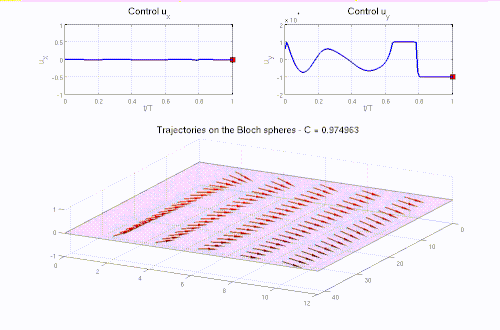
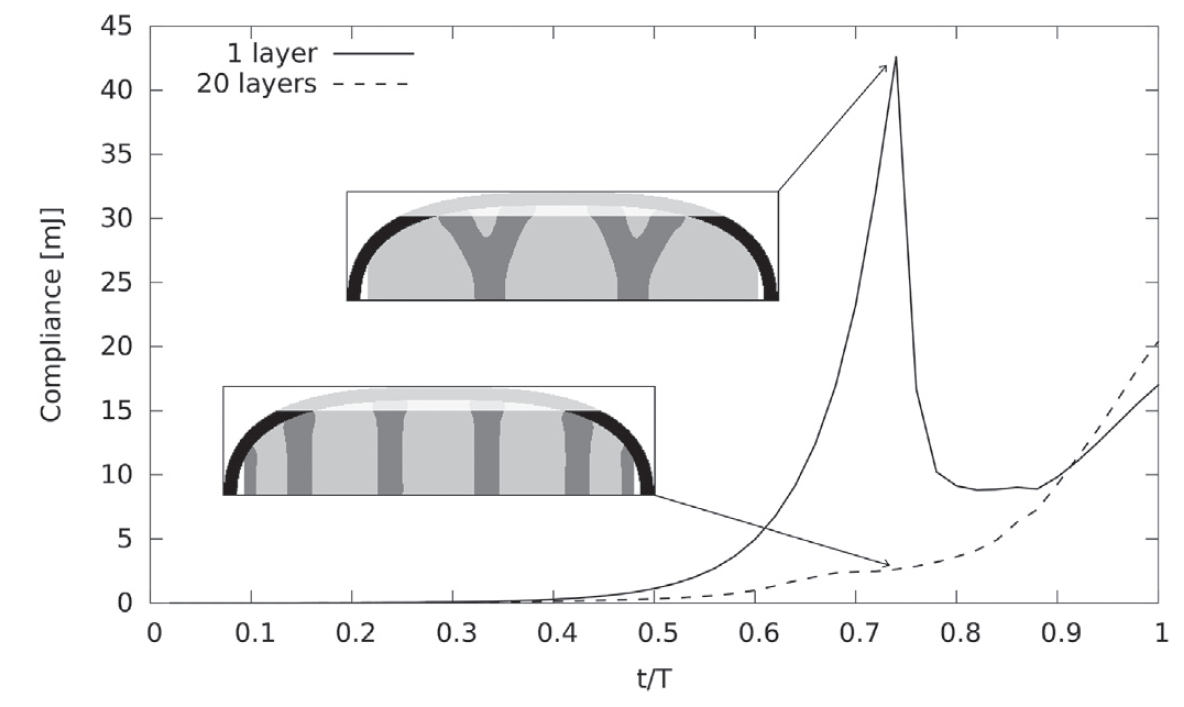
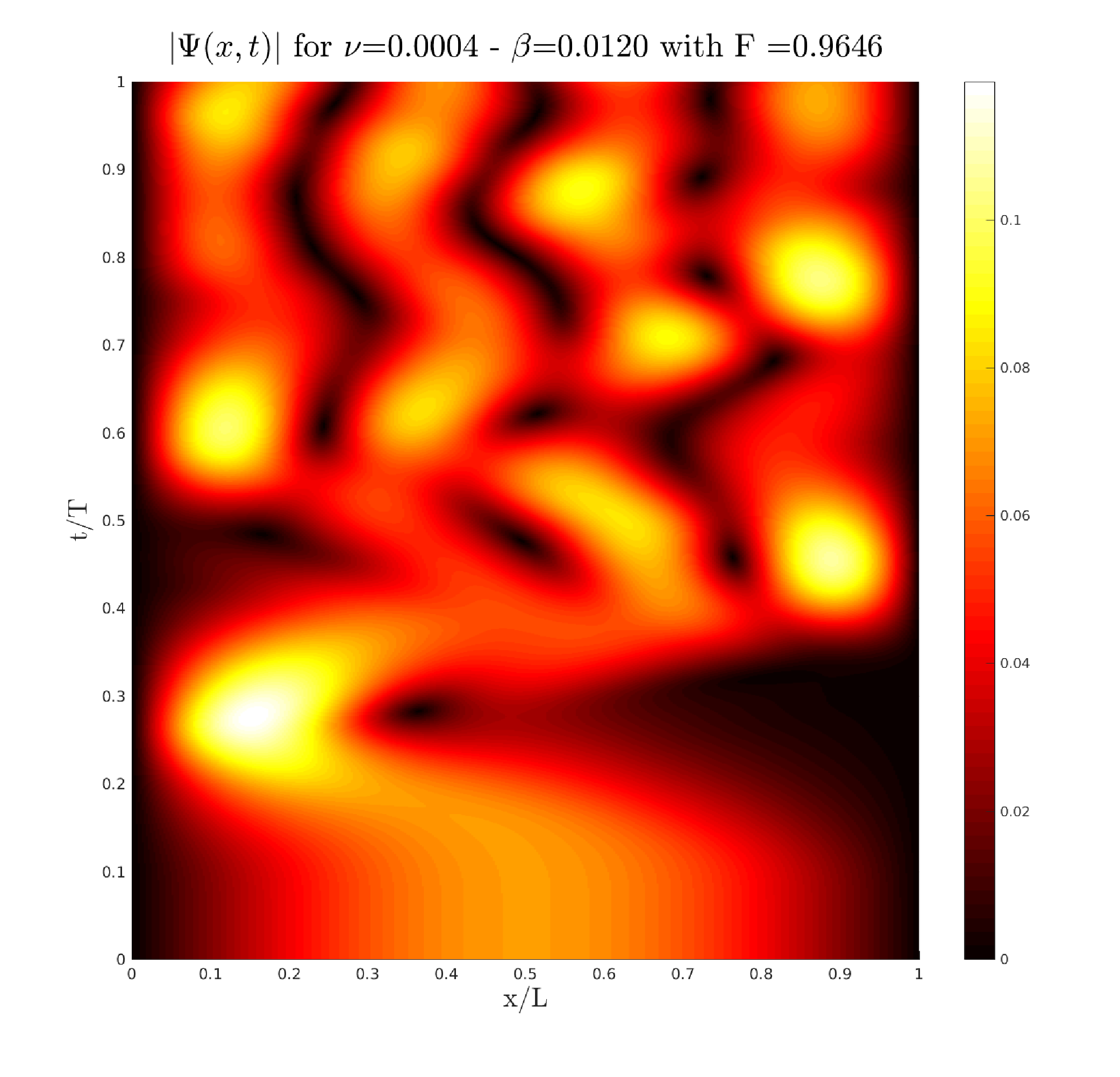
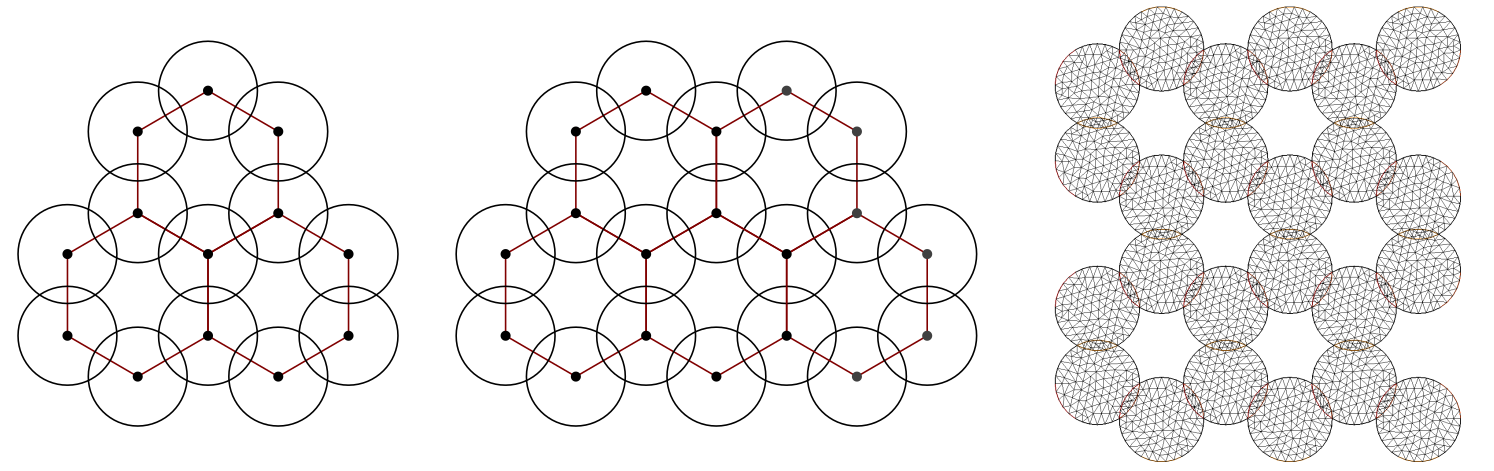
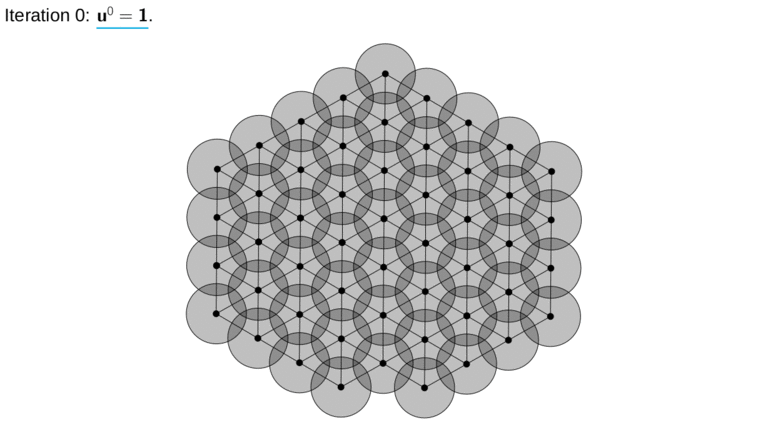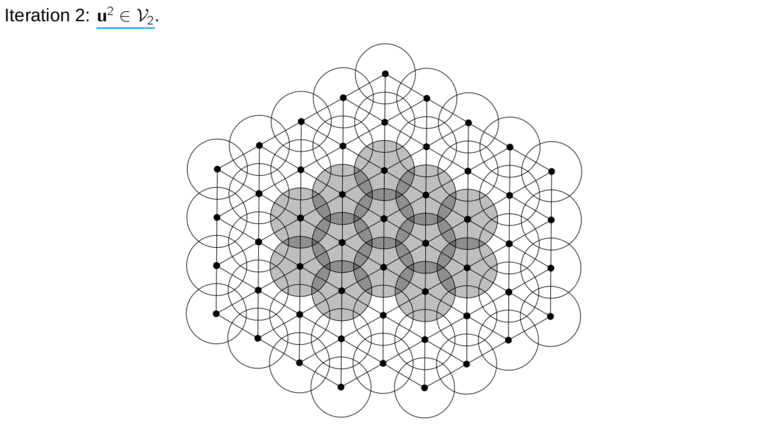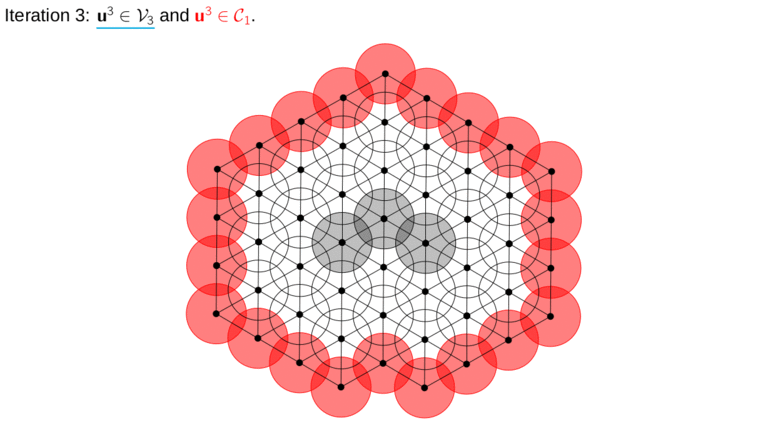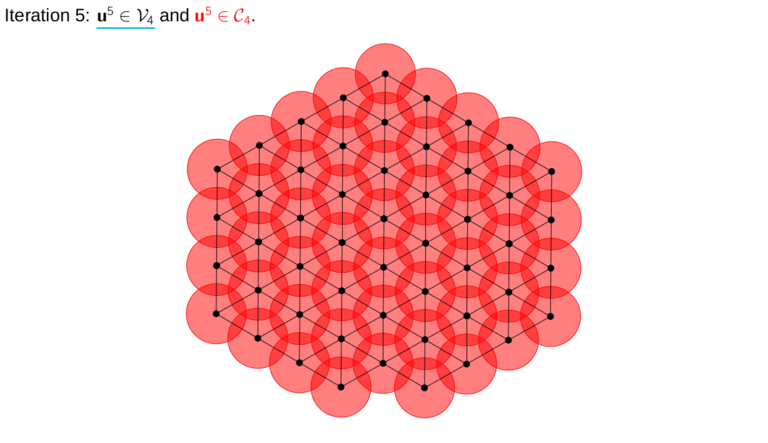
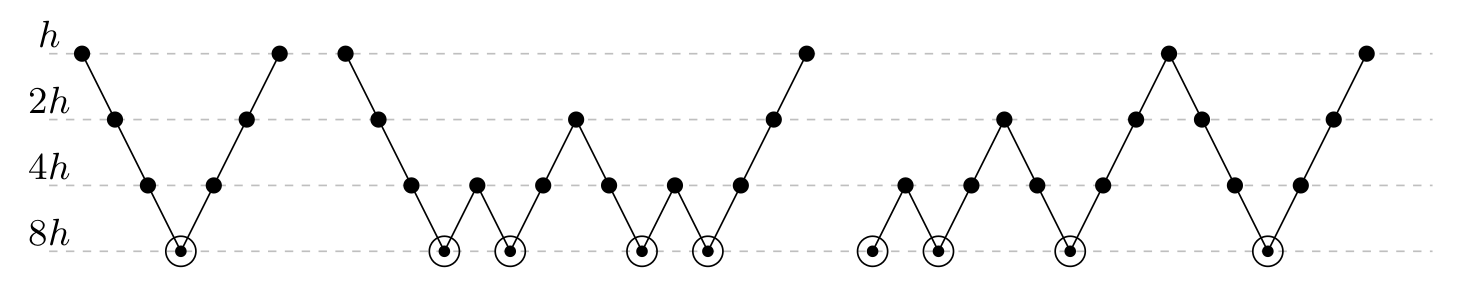
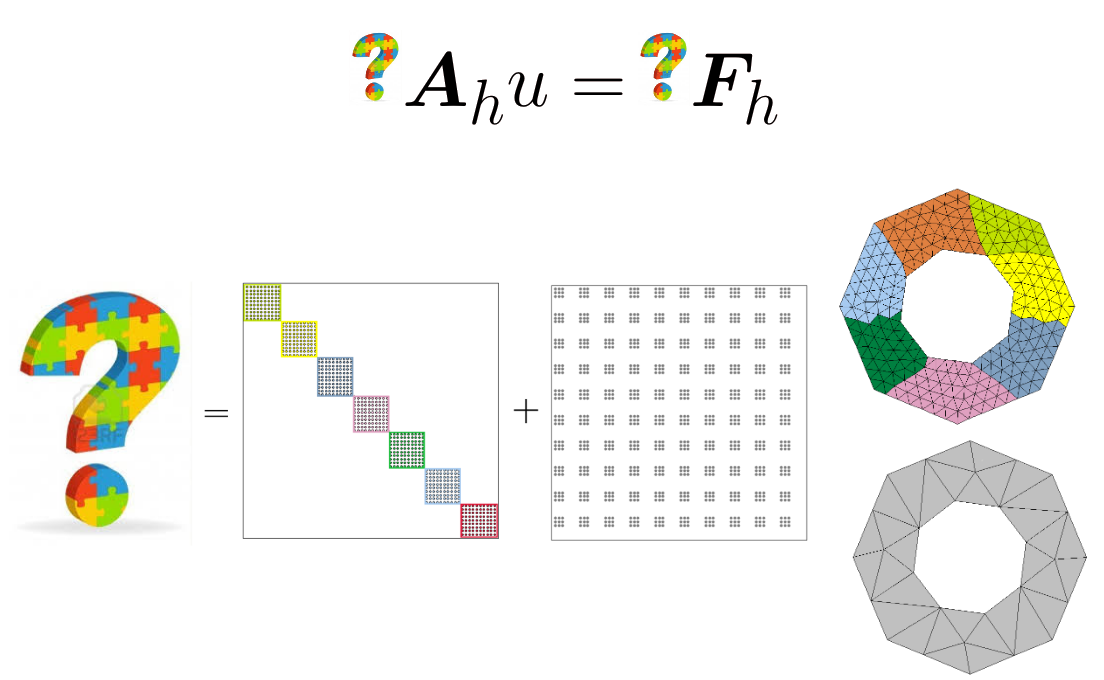
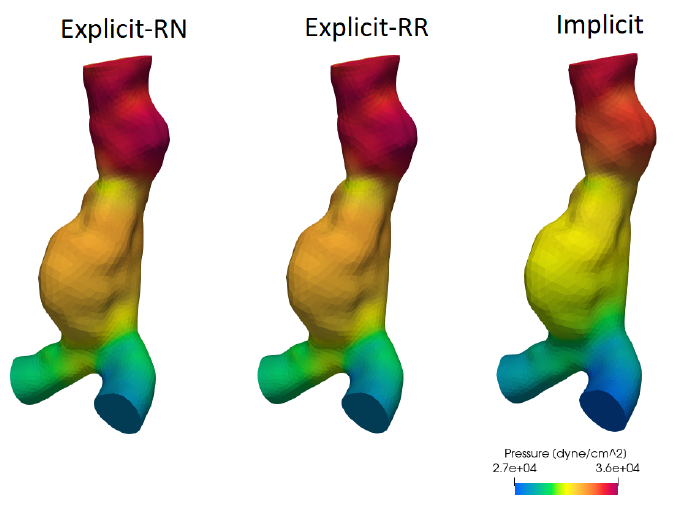
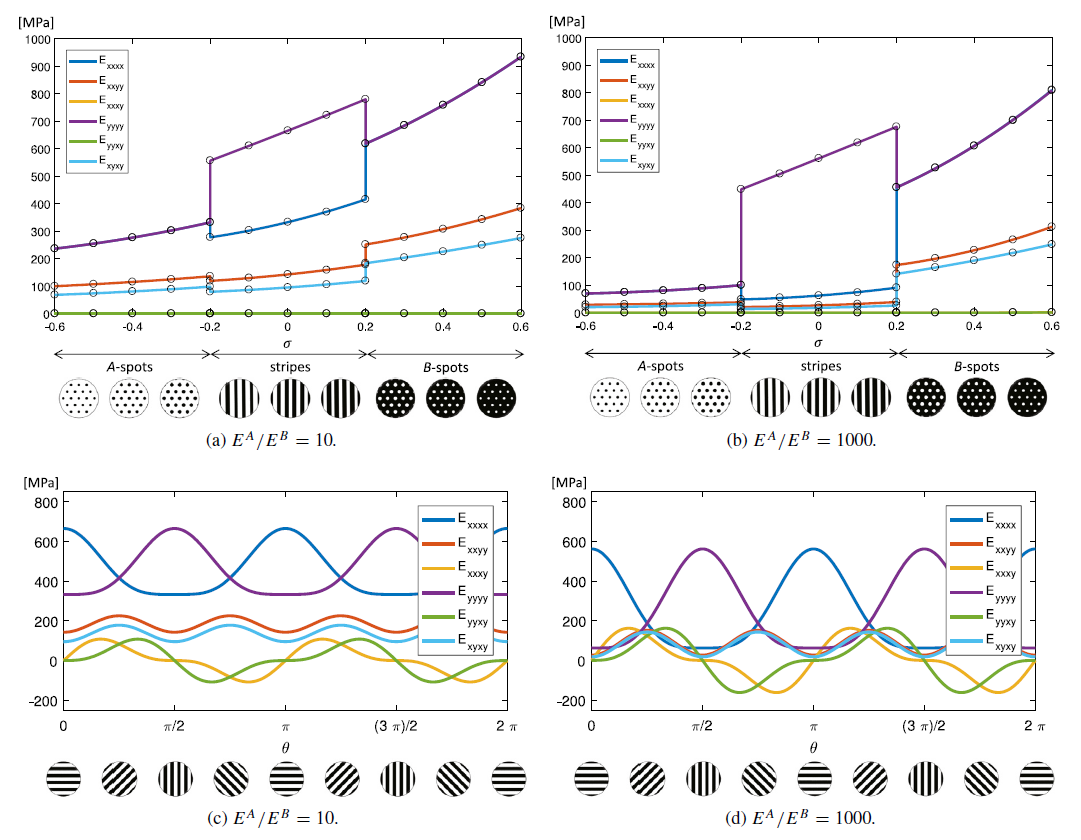
Real-life applications driven by engineering, industry and natural sciences are giving an ever-increasing boost to the development of innovative methods for the numerical modeling of differential problems, optimization, fast solution techniques and model order reduction. These are the main pillars of the MOX Research Group for Advanced Numerical Methods for Scientific Computing:
- Numerical modeling of PDEs for multi-physics, multi-scale and hybrid-dimensional problems
- Numerical optimization
- Fast solution techniques for large-scale problems
- Reduction of complexity and uncertainty